A estatística possui um ramo chamado, estatística descritiva, responsável por sumarizar e descrever conjuntos de dados. Nesse artigo vamos aprender como utilizar algumas medidas como: média, mediana e moda.
Para entender os conceitos e como calcular cada um dos conceitos vistos nesse artigo, vamos utilizar um exemplo base:
Entrevistamos um conjunto de 15 pessoas com o objetivo de identificar se aquelas que tinham curso superior, recebiam um salário melhor.
Essas pessoas foram convocadas aleatoriamente para responder ao questionário que perguntava qual o rendimento dela no ano de 2017. Para facilitar nossos cálculos utilizamos os valores arredondados para milhares de reais.
O resultado do questionário resultou nos seguintes dados: 110, 25, 50, 50, 55, 30, 35, 30, 4, 32, 50, 30, 32, 74, 60.
1. Como calcular a média aritmética?
Dado um conjunto de observações para calcular a média aritmética você deve somar os seus valores e dividir pelo número de observações.
O cálculo acima mostra que a média de rendimentos por ano das 15 pessoas questionadas foi de 44,4 o que equivale a R$ 44.400,00 reais. Se retirarmos a pessoa com rendimento anual de R$110.000,00, a média das 14 pessoas restantes ficará R$ 39.700,00. Se essa pessoa com o rendimento atípico for adicionada ao grupo o valor da média aumentara R$ 4700,00. Veja que no exemplo acima a média em questão é sensível à influências de observações extremas, desta forma ela não é considerada uma medida resistente.
Saiba mais em nosso post Média Simples e Média Ponderada: O Que É e Como Calcular? 📊
2. Como calcular a mediana?
A mediana M é o ponto central de uma distribuição, desta forma metade das observações são menores que a mediada e metade das observações são maiores que a mediana. Para fazer o calculo da mediana você deve seguir os passos:
- Ordene as observações do menor valor para o maior valor.
- Se o número de observações for um número ímpar a mediana é a observação (valor) central dessa lista ordenada. Para achar a mediana, faça (n + 1)/2 onde n é o número de observações.
- Exemplo de mediana: considerando os 15 rendimentos anuais vistos anteriormente o calculo da mediana pode ser feito da seguinte forma:
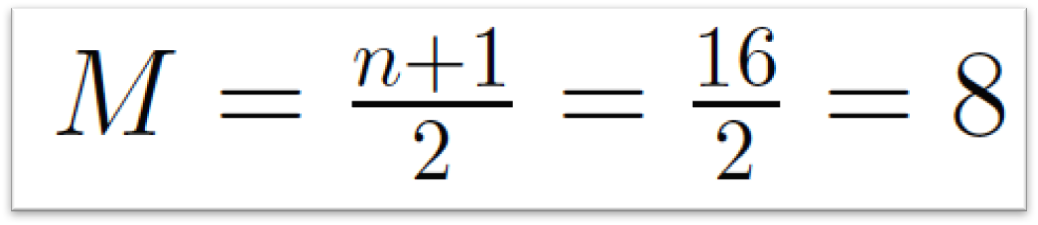
OBS.: note que a mediana é a oitava observação da lista ordenada.
- Se o número de observações for um número par a mediana M é a média das duas observações centrais na lista ordenada. A mediana será (n + 1)/2 a partir do valor mais baixo da lista.
- Exemplo de mediana: retirando o valor atípico da lista anterior (110) a lista ficará com 14 observações, são elas: 4 25 30 30 31 32 35 50 50 50 55 60 74
OBS.: a mediana é o ponto médio entre as observações (33,5). Para localizar o ponto medio na lista basta aplicar a formula (n + 1)/2, no exemplo acima 7,5 é a localização do ponto médio (entre a sétima e a oitava observação na lista ordenada).
Saiba mais em nosso post sobre Mediana: O Que É, Como Calcular e Sua Importância
3. Diferenças entre Média e Mediana
3.1. Definição e Sensibilidade a Valores Extremos
- Média:
- Calculada pela soma de todos os valores dividida pelo número de elementos.
- Influenciada por valores extremos (outliers), podendo distorcer a interpretação dos dados.
- Exemplo: Em um conjunto com salários muito altos, a média pode ficar artificialmente elevada.
- Mediana:
- Representa o valor central quando os dados estão ordenados.
- Não é afetada por outliers, sendo mais robusta em distribuições assimétricas.
- Exemplo: Em análises de renda, a mediana reflete melhor a realidade da maioria.
3.2. Representação dos Dados
- Média:
- Indica um “ponto de equilíbrio” matemático do conjunto.
- Útil quando os dados têm uma distribuição simétrica e sem valores atípicos.
- Mediana:
- Mostra o valor que divide os dados em duas partes iguais.
- Melhor para conjuntos com grandes variações ou distribuições enviesadas.
3.3. Quando Usar Cada Uma?
- Use a média quando:
- Os dados têm uma distribuição uniforme.
- Não há outliers significativos.
- O objetivo é obter um valor representativo para cálculos futuros.
- Use a mediana quando:
- Há valores extremos que podem distorcer a análise.
- A distribuição é assimétrica (ex.: renda, preços de imóveis).
- O foco é entender a tendência central sem influência de outliers.
De forma resumida, a média ajuda em cálculos e comparações gerais, enquanto a mediana é mais confiável em dados desbalanceados. Em muitos casos, o ideal é analisar ambas as medidas para ter uma visão mais completa.
Como calcular a moda?
É chamado de moda a observação (valor) que é mais frequente no conjunto analisado. Voltando para o nosso exemplo temos: 110 25 50 50 55 30 35 30 4 32 50 30 32 74 60. Observe que três pessoas receberam rendimento de 30, três pessoas receberam 50, duas pessoas receberam 32. Percebam que os números 30 e 50 se repetem três vezes cada um. Isso significa que o conjunto possui duas modas (30 e 50) e é chamado de bimodal.
Experimente grátis o FastFormat
Além da formatação automática, o FastFormat conta com vários recursos para facilitar a construção de seus trabalhos acadêmicos. Acesse agora!


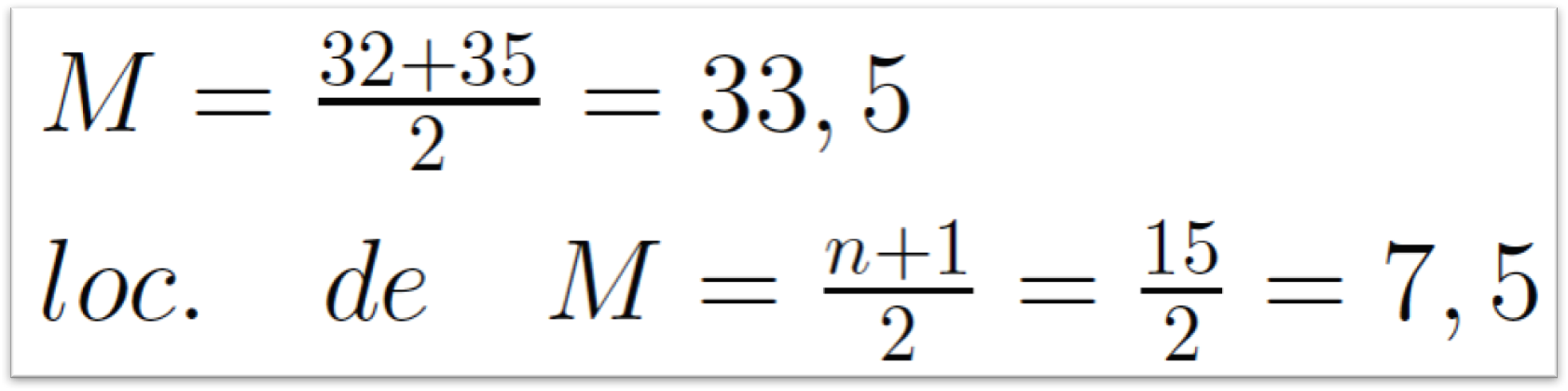



Add comment